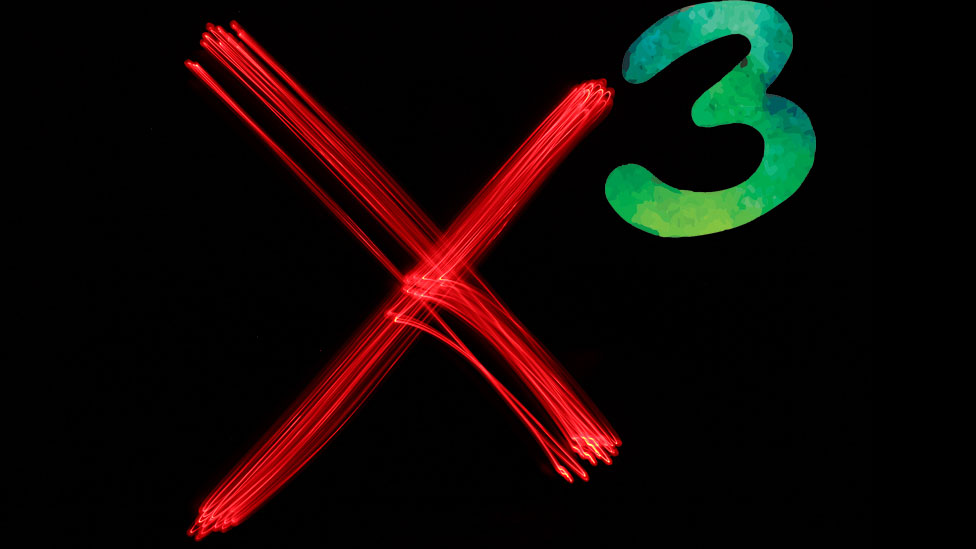La leyenda dice que Qin Jiushao era una suerte de canalla.
Pero también fue "uno de los más grandes matemáticos de su época y, de hecho, de toda la historia", como escribió el padre de la Historia de la Ciencia George Sarton.
Aunque no hay una biografía del peculiar personaje en Sòng Sh? -que registra la historia de la dinastía Song (960-1279)-, los expertos han reconstruido su historia valiéndose de fragmentos de información recopilada.
Documentos como una carta enviada al emperador en la que Qin es descrito por uno de sus contemporáneos como"... tan violento como un tigre, o un lobo, y tan venenoso como una víbora o un escorpión".
Sabemos que...
Nació en Sichuan, China, hacia 1202.
En su juventud estudió en la Junta de Astronomía en Nan Sung y luego fue instruido por un recluso, como él mismo cuenta en el prefacio de su famosa obra Shushu Jiuzhang o "Tratado de matemáticas en nueve capítulos" (1247).
El libro, además de ser valioso por los temas puramente matemáticos, tiene comentarios prácticos, de manera que provee información preciada acerca de las condiciones sociales y económicas en China durante el siglo XIII.
También sabemos que...
Fue un mandarín (burócrata) imperial fantásticamente corrupto que saltó de un cargo a otro, pues constantemente lo descubrían haciendo fechorías.
- Como administrador en Qizhou (ahora Qichun) en la provincia de Hupeh, su comportamiento fue tan terrible que causó una revuelta militar.
- Luego fue nombrado gobernador de Hui-chou (ahora She-hsien) en la provincia de Anhwei, donde era responsable por el comercio de sal, de manera que aprovechó para venderla ilegalmente y se hizo muy rico.
- Fue destituido de su cargo como gobernador de Qiongzhou en Hainan en 1259 por corrupción y explotación después de 100 días en el puesto y regresó a su hogar tras haber adquirido una inmensa riqueza de manera ilegal.
- A pesar de su historial, logró obtener un cargo como asistente en el distrito de Yin (cerca de Ningpo) en Zhekiang, pero, en 1260, nuevamente por corrupción, Qin fue enviado a Meizhou (ahora Meixian), el lugar en el que poco después murió.
Talentoso
La información que quedó de él muestra que además de su afición por la malversación de dinero del gobierno, Qin tenía el hábito de envenenar a cualquiera que se interpusiera en su camino.
Pero también habla de un hombre con un enorme talento en muchas áreas.
Según el escritor Chou Mi (1232-1298), no solo era "por naturaleza, extremadamente ingenioso", sino que conocía a profundidad "la astronomía, harmonía, poesía y hasta arquitectura".
"Respecto a los deportes -jugar polo, tiro con arco, manejo de la espada- no había nada que no pudiera aprender".
Y a todo esto se le agrega otra faceta: la de guerrero.
Durante 10 años, luchó contra los invasores mongoles, pero a lo largo de gran parte de ese tiempo se quejó de que su vida militar lo alejaba de su verdadera pasión.
Las matemáticas.
Incógnitas elevadas a la 3ª potencia
Qin trató de resolver ecuaciones que surgen al tratar de medir el mundo que nos rodea.
Las ecuaciones cuadráticas involucran números que están al cuadrado, o con la potencia de dos, como 5 x 5.
Los antiguos mesopotámicos ya se habían dado cuenta de que estas ecuaciones eran perfectas para medir formas planas y bidimensionales, como un plaza.
Pero Qin estaba interesado en ecuaciones más complicadas: las cúbicas.
Estas involucran números que están elevados a la potencia de tres -por ejemplo: 5 x 5 x 5-, que son las indicadas para medir formas tridimensionales.
Qin encontró una forma de resolverlas que funcionaba así:
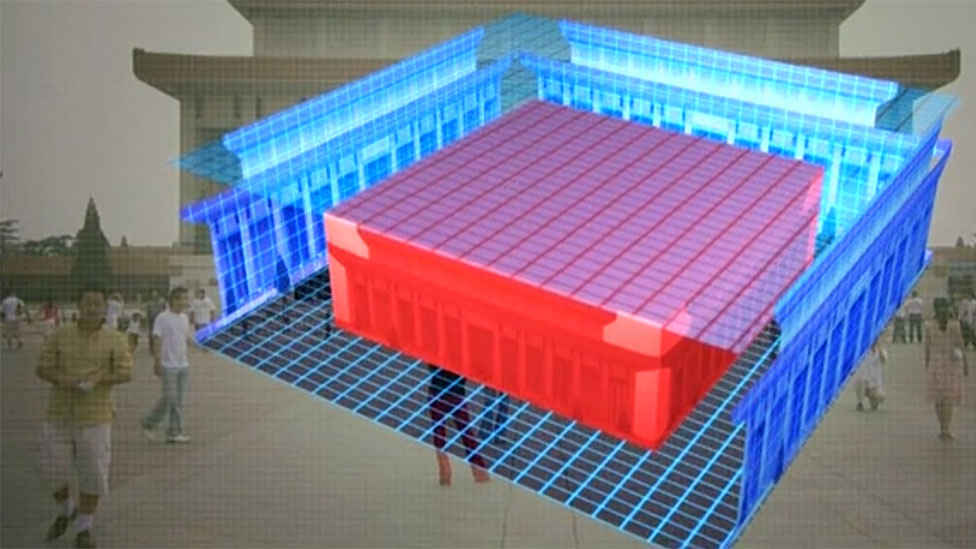
Digamos que Qin quiere saber las dimensiones exactas del mausoleo del presidente Mao.
Sabe cuál es el volumen del edificio y las relaciones entre las dimensiones.
Para obtener su respuesta, Qin usa lo que sabe para producir una ecuación cúbica. Luego hace una conjetura educada en las dimensiones.
Aunque ha abarcado una buena proporción del mausoleo, todavía faltan trozos del espacio.
Qin toma estos trozos y crea una nueva ecuación cúbica.
Así puede refinar su primera suposición tratando de encontrar una solución a esta nueva ecuación cúbica, y así sucesivamente.
Cada vez que hace esto, las piezas que le quedan se hacen cada vez más pequeñas y sus conjeturas son más cercanas a la respuesta exacta.
4 siglos antes que Newton
Lo sorprendente es que el método de Qin para resolver ecuaciones no fue hallado en Occidente hasta el siglo XVII, cuando Isaac Newton creó un método de aproximación muy similar.
El poder de esta técnica es que se puede aplicar a ecuaciones aún más complicadas.
Qin incluso usó sus técnicas para resolver una ecuación que involucra números elevados a la potencia de 10.
Fue algo extraordinario; matemáticas muy complejas.
Pero aunque Qin se adelantó años a su tiempo, había un problema con su técnica: solo nos da una solución aproximada.
Eso puede ser lo suficientemente bueno para un ingeniero, pero no para un matemático.
Las matemáticas son una ciencia exacta y Qin no pudo encontrar una fórmula que le diera una solución exacta a esas complicadas ecuaciones.
Qin murió circa 1261. Fue uno de los grandes de la Edad de Oro de las matemáticas chinas, en la que el Imperio dio enormes saltos en esta ciencia.
Los próximos grandes avances tendrían lugar en un país que se encuentra al suroeste de China, una nación con una rica tradición matemática que cambiaría todo para siempre: India.